The Harmonic Lattice
By Richard Merrick
Originating in the quantum theory of Max Planck, the Quantum Chromodynamic Lattice (Lattice QCD) is the scientific name for what is popularly known as the holographic universe, zero-point lattice, the field, the divine matrix, crystallized space, quintessence or just ‘the aether.’ Planck was convinced of the existence of this underlying structure in nature, once declaring:
‘All matter originates and exists only by virtue of a force… We must assume behind this force the existence of a conscious and intelligent Mind. This Mind is the matrix of all matter.’
In fact, Planck’s quantum matrix idea was the actual inspiration behind ‘The Matrix’ movies. While it sounds more like science fiction than science fact, the idea is anything but fiction.
Recent advances in the field of high energy physics are yielding solid evidence of an ‘auxiliary fifth dimension’ acting as a kind of ‘quantum aether’ underneath classical physics. Some of the latest research papers can be found (not surprisingly) on the Los Alamos National Laboratory web site. Their library includes such titles as:
• QCD phase diagram: an overview
• Understanding nucleon structure using lattice simulations
• Advances and applications of lattice supersymmetry
• Deconfining Phase Transition on Lattices with Boundaries at Low Temperature
And my favorite:
• 2+1 flavor domain wall QCD on a (2 fm)^3 lattice: light meson spectroscopy with Ls = 16
While these papers all sound pretty complicated, they are based the simple idea that all atoms are really a sphere locked inside a cubically structured space rather than just a freestanding sphere in an empty vacuum as commonly taught. Other papers on the subject (such as Rauscher-Haramein Theory) concur, going so far as to describe atoms as ‘breathing’ between tetrahedral and cubic configurations to form a cuboctahedron in between. The notion of a cubic structure behind atomic spin came from the realization early on in quantum theory that atoms with an even number of electrons are more stable than ones with an odd number. This was found to be especially true for atoms having 8 electrons in the ‘L shell’ since they orbit symmetrically to form the corners of a cube. When you consider that a cube is the best shape to fill space perfectly, it makes perfect sense.
The Lattice QCD is generally described as follows. Each cube has side length of about 1.26 fermions (fm) and cubic volume of 2 fm. This is then cubed to produce the space of four connected cubes, totaling a volume of 8 fm, which is then doubled to produce eight connected cubes with a combined volume of 16 fm (thus the ‘Ls = 16’ in the title above). This is easily visualized as a spatial lattice having 27 equally spaced and interconnected points (or vertices) as shown in the following diagram.
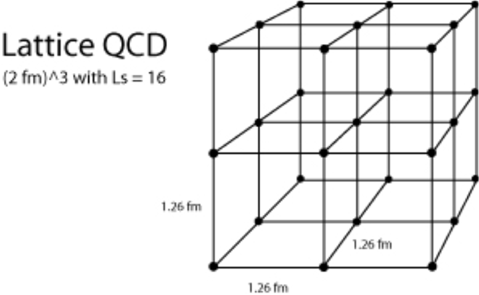
To understand how it contains energy, just imagine a large number of these cubes joined together to create a cage that you could hold onto and shake. As you rattle the cage, energy flows into it and reflects around inside, sometimes aligning in perfect resonance with the lattice and other times creating a canceling pattern of interference. If we made this cage many times bigger, the rattling would turn into spherical ripples and intersecting tides of energy flowing through the lattice like currents in an ocean. As fractional waves cancel out and simple whole number proportional waves reinforce one another, stable standing waves emerge and harmonics emerge to piggyback for any given frequency.
At each intersecting point of the vibrating lattice, a tiny spiraling black hole is thought to form. This is based on the idea that the lattice resonates like a crystal (cooling, contracting and imploding from the Big Bang), causing miniscule swirling vortices to form at each point in the space lattice. It is further hypothesized that these vortices follow a golden spiral, or Spira Mirabilis, something like a chambered nautilus or spiral galaxy. It could well be that all space is uniformly perforated by such vortices and it is from this polarizing effect that spirals form at all scales of nature. Few realize that their body and brain may be bathed in this perforated space and even interconnected and able to communicate through these infinite black holes.
Now, when ripples of energy align in the center of the cubes, crystallized harmonic matter called fermions are said to form. These particles include protons, electrons, quarks and leptons – all spinning in a locked cubic structure. But, when ripples align with the damping points of the lattice itself, energy particles called bosons continue to travel outward in waves, spinning off the vortices that propel them through the lattice. This includes photons of light, radio waves, x-rays, gamma waves, cosmic waves and gravity – all traveling in between particles of matter. Throughout the entire lattice, the reverberation of zero-point boson energy is believed to be the invisible force that keeps electrons spinning in their orbits and nuclear particles bound together. Without it, everything would simply fall apart.
It is through this idea of a continuously resonating space lattice that the ancient idea of a musical universe is reborn – Pythagoras’ musica universalis and Robert Fludd’s mythical celestial monochord – all out of a primordial balance between spherical harmonic resonance and infinite damping spirals. Philolaus, a ‘most ancient’ follower of Pythagoras, referred to this in the opening of his book Peri physeos, or On Nature:
‘Nature in the cosmos is composed of a harmonia between the unlimited and the limited and so too is the whole cosmos and everything in it.’
Philolaus goes on to describe Pythagoras’ attempt to get to the bottom of this universal ‘harmonia’ by trying to split a wholetone interval like a musical atom. Expecting to prove the universal principle of simple harmonic proportions, Pythagoras was surprised (embarrassed really) to find that the wholetone ratio of 9:8 could only be reasonably factored into an awkward 27 parts. Of course, this corresponds to the 27 damping points in the Lattice QCD model of cubic space.
When we take the proportion 9:8 / 27 = 0.04166667, which Pythagoras called a ‘comma,’ and divide it into the lattice volume of 16, the result is an even 384 ‘musical sub-cubes’. Each of the eight lattice cubes then contains 48 such musical sub-cubes, each having a volume of exactly 9:8 / 27 = 0.04166667 fermions. Is this identical scaling proportion a mere coincidence or is it real evidence of spherical harmonics spinning out of the infinite holes in the Lattice QCD like some kind of fractal music? Pythagoras was right when he said: ‘There is geometry in the humming of the strings, there is music in the spacing of the spheres.’
We find many more such correlations between Lattice QCD and music. For instance, a musical tone produces higher frequency harmonics at whole number multiples (2X, 3X, 4X, 5X, etc.) while the spacing of electron shells follows the same proportions around an atomic nucleus. It is a scientific fact that electrons are spaced harmonically around their atomic nucleus.
Furthermore, the even harmonics of a musical tone (2X, 4X, 6X, etc.) resonate in perfect alignment with a fundamental frequency to form octaves in pitch space in the same way evenly aligned fermions (material particles) resonate to form cubic octets in physical space. Against this perfect symmetry are then the odd harmonics of a tone (3X, 5X, 7X, etc.) that shape the timbre of sound just as odd bosons provide the binding force to carve energy into material shapes. Without a doubt, the same harmonic principles of resonance are at work in both music and the quantum space lattice.
In his book Harmonograph: A Visual Guide To The Mathematics of Music, author Anthony Ashton shows us how musical ratios interact to create geometric figures. Using a 19th century device called a harmonograph, Ashton set the frequencies, rotational direction and amplitudes of two vibratory arms connected to a pendulum ink pen to draw an assortment of shapes on paper. When the vibrating arms were concurrent (vibrating in the same direction), the pen drew a variety of nested circles and cardioid or heart shapes. But when the vibrations were countercurrent (moving in opposite directions), the pen drew triangles (octave), squares (double octave), pentagons (perfect fifth), septagons (perfect fourth) and so on. When an open phase was used, spirals (unison), shells and eggs (near unison) were drawn.
These geometric patterns of harmonic resonance are also found on vibrated plates of sand, powder in water and even plasma jets. More recently, they have been demonstrated to occur in spinning buckets of water, in the eyes of powerful hurricanes and beyond the Earth on other planets and in stellar clouds. Caused by the interplay between harmonic resonance and damping in all standing wave systems, the same simple geometrical shapes occur everywhere and in everything, whether animate or inanimate.
It’s easy to see from all these examples how energy spins recursively into larger and larger harmonic forms – all contained inside a shared and continuously resonating space lattice. As energy reflects back on it self inside this lattice, it cannot help but create the same regular geometrical shapes. Inanimate matter will always crystallize into the countercurrent shapes of squares, pentagons, hexagons, octagons and other regular geometries while life follows the concurrent polar forms of circles, ellipses, eggs, shells and cardioids. All of these shapes emerge from the very same harmonic behavior found in a vibrating guitar string.
When we listen carefully to music, we can hear the polyhedrons of mineral crystals and the cardioids of life represented in the harmonic interference patterns of musical scales, chords and melodies. Since our body and brain grew inside this lattice, we are imbued by it with the ability to instantly recognize, measure and enjoy complex timbres and musical harmonies. As the music is carried through this lattice by compression waves of air molecules, we instinctively follow and anticipate the directional flow of energy in each combination of tones with absolutely no effort at all. From simple auditory shapes to vast symphonic landscapes of sound, music projects our dreams through the holonomic lattice of our brain while quantum energy projects our reality through the holographic lattice of space. Music is our personal laboratory for the study of structured space.
In the final analysis, modern Lattice QCD theory is really just a sequel to the Pythagorean Music of the Spheres that once described everything – atoms, plants, animals and planetary orbits – as a musical harmony of spherical waves. This always has and always will be the easiest way to grasp the form, function and beauty of our fifth dimension. With the growing popularity of Lattice QCD, it is only a matter of time now before science and society will once again hear the music of the quantum lattice.
