Sacred Geometry

By Richard Merrick

Harmonic Visualization Models – Sacred Geometry

The study of sacred geometry was passed down over thousands of years from the ancient mystery schools. The most common geometries considered sacred are the Egyptian Flower of Life, the Hebrew Vesica Piscis and the Italian Borromean Rings (also known as the Holy Trinity), though there are others.

The reason such geometry was considered sacred is due to their similarity to organic geometries found in life. Such geometry was described as ’emanations’ by Gnostics, indicating their awareness that they were patterns formed by the intersection or interference patterns of waves. And since music travels in waves, sacred geometry became intertwined with musica universalis, the ancient theory of everything. Through musical proportions, everything could be modeled using sacred geometry.

To see how this works, consider the following musical Chromatic Ring divided into twelve equal sections according to the earlier harmonic color model. This is known as the Z/12Z cyclic ring model where Z is the set of integers 1 through 12.

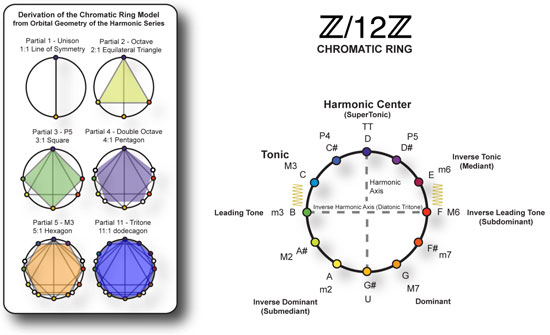
The labels indicate bi-lateral symmetry between each half of the ring as divided by the Harmonic Axis through the Harmonic Center or harmonic Partial 9. Spring symbols are used to indicate the regions where harmonics share energy, namely between the tritone and tonic major third.

From the Chromatic Ring, a dual ring system can be used to geometrically represent the standard Fourier wave consisting of complementary wave components sine and cosine in phase-quadrature (out of phase by 90-degrees).

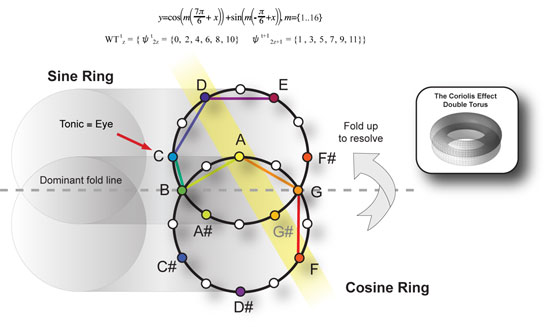
To the ancients, this interlocking ring arrangement was known as the Vescia Piscis or Mandorla (meaning ‘almond’), referring to the union section of the two rings. In the Hebrew Kabbalah, all life is described as entering into the world through the mandorla interference region between the dual rings.

In the most general sense, this is correct. The dual rings are a vertical cross-section of the double torus produced by the Coriolis effect – a geometry found in the formation of galaxies and our own solar system. Life too is toroidal like a hurricane, twisting around an axis, as seen in the swirl of hair at the crown of the head. When we are born, the birth canal is indeed a mandorla.

For these and other reasons, the mandorla is used to frame religion icons and deities in Christianity, indicating their origination from the creation matrix.

Moving beyond religious interpretations, we can better understand the physical properties of the dual rings by separating the twelve tones into two groups of six divided between the rings – one group in the top ring to represent sine components in phase with the Harmonic Center (D for harmonic series of C) and another group in the bottom ring to represent the complementary cosine components. The two groups of tones are known as whole tone scales, of which there are only these two.

Interestingly, we find that the mandorla corresponds to the so-called ‘dominant’ interval (e.g., {G, B} in C major), used in common practice music to create tension and resolve to the tonic. This so-called ‘dominant-tonic’ resolution is also used as a central element in music harmony to chain together a series of chords into what is called the Cycle of Fifths. When represented as a lattice of interlocking Vesica Piscis, dominant triads can be seen to cascade through an orbit of twelve tones.

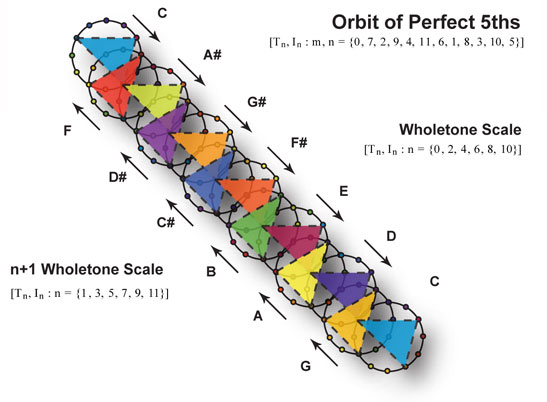
When this same lattice progression is then transformed onto an orthogonal wave lattice using dominant 7th chords, something truly amazing happens. The Cycle of Fifths traces out the profile of a fish. In fact, the tense leading tone adds onto itself in such a way as to produce a prominent fin-like geometry – appearing very shark-like. Sacred geometry indeed!

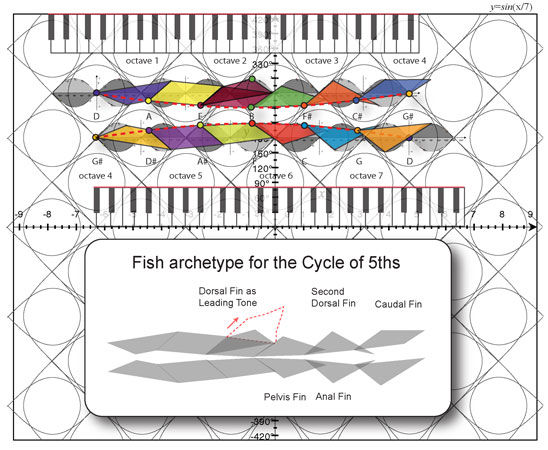
Not only is life is born through a mandorla, but harmony of form is the inevitable self-organization process of nature. As harmonic waves reflect inside round containers, they assume the same proportional shapes found in Z/12Z music harmony – a bi-lateral symmetry of harmonic proportion. Sacred geometry is nothing less than the visualization of physical musical concepts.